大容量コンデンサーを用いた実験(3)
静電エネルギー
1 目的:
手回し発電器を接続したコンデンサーを放電させ、そのハンドルの回転数から蓄えられた静電エネルギーを定量化し、静電エネルギー・電気容量・充電電圧の関係を調べる。
2 準備:
大容量コンデンサー(1F、0.5F、0.25F)、手回し発電器、直流電圧計、リード線、グラフ用紙
3 理論:
コンデンサーに蓄えられる静電エネルギーは、U=1/2CV2と表される。静電エネルギーU[J]は手回し発電器の回転数n[回]に比例することから、これを測定すれば、静電エネルギーU[J]が充電電圧V[v]の2乗に比例することや電気容量C[F]に正比例することが確認できる。
4 実験操作:
(1) 下の図のように、コンデンサー、手回し発電器、電圧計をリード線で接続する。

(2) 手回し発電気を回してコンデンサーを充電し、電圧計の目盛りが7.0v程度になったらハンドルから手を放す。充電する際、コンデンサーの耐電圧以上に電圧が加わらないように注意する。
(3) ハンドルの回転が安定するように、発電器をまっすぐ保持する。
(4) しばらくすると電圧計の目盛りがV=6.0[v]まで下がってくる。このときから、放電が終わるまでのハンドルの回転数を数える。
(5) 同様にして、5.5v〜1.0vの充電についてもハンドルの回転数を数える
(6) 静電容量の異なったコンデンサーについても同様にして実験をする。

5 実験結果の記録:
電気容量C=( )F
| 充電電圧V[V] |
1.0 |
1.5 |
2.0 |
2.5 |
3.0 |
3.5 |
4.0 |
4.5 |
5.0 |
5.5 |
6.0 |
| ハンドルの回転数n[回] |
|
|
|
|
|
|
|
|
|
|
電気容量C=( )F
| 充電電圧V[V] |
1.0 |
1.5 |
2.0 |
2.5 |
3.0 |
3.5 |
4.0 |
4.5 |
5.0 |
5.5 |
6.0 |
| ハンドルの回転数n[回] |
|
|
|
|
|
|
|
|
|
|
電気容量C=( )F
| 充電電圧V[V] |
1.0 |
1.5 |
2.0 |
2.5 |
3.0 |
3.5 |
4.0 |
4.5 |
5.0 |
5.5 |
6.0 |
| ハンドルの回転数n[回] |
|
|
|
|
|
|
|
|
|
|
6 考察:
(1) 横軸にV[V]、縦軸にn[回]をとって、得られた測定値を記入し、それらの点をなめらかに結んでグラフをつくれ。
(2) コンデンサーに蓄えられた静電エネルギーと充電電圧との間には、どのような関係があるといえるか。グラフから考察せよ。
(3) コンデンサーを充電する際、充電電圧(電圧計の読み)と手回し発電器の手ごたえや、回転速度について気付いたことを記せ。
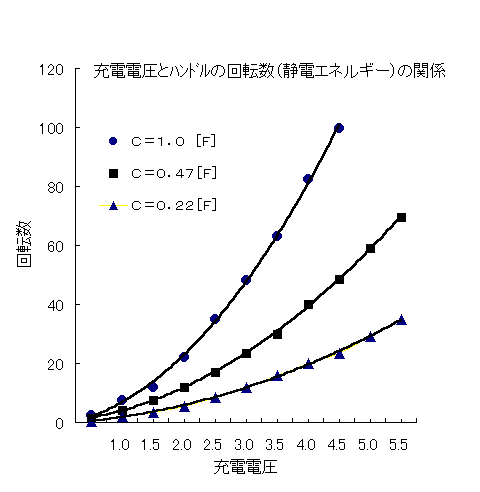
7 実験結果例
電気容量C=( 1.0)F 耐電圧5.0V
| 充電電圧V[V] |
1.0 |
1.5 |
2.0 |
2.5 |
3.0 |
3.5 |
4.0 |
4.5 |
5.0 |
5.5 |
6.0 |
| ハンドルの回転数n[回] |
2.5 |
7.5 |
12.0 |
22.0 |
35.0 |
48.0 |
63.0 |
82.5 |
99.5 |
- |
- |
電気容量C=(0.47)F 耐電圧10V
| 充電電圧V[V] |
1.0 |
1.5 |
2.0 |
2.5 |
3.0 |
3.5 |
4.0 |
4.5 |
5.0 |
5.5 |
6.0 |
| ハンドルの回転数n[回] |
1.5 |
4.0 |
7.5 |
12.0 |
17.0 |
23.5 |
30.0 |
40.0 |
48.5 |
59.0 |
69.5 |
電気容量C=(0.22)F 耐電圧10V
| 充電電圧V[V] |
1.0 |
1.5 |
2.0 |
2.5 |
3.0 |
3.5 |
4.0 |
4.5 |
5.0 |
5.5 |
6.0 |
| ハンドルの回転数n[回] |
0.5 |
2.0 |
3.5 |
5.5 |
8.5 |
12.0 |
16.0 |
20.0 |
23.5 |
29.0 |
35.0 |