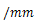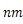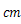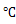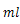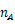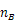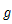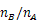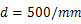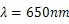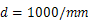回折格子に単色光を当てて、円形スクリーンに投影すると、明暗の縞模様が見られる。このとき、単色光の波長
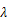 と、1次の回折像の回折角
と、1次の回折像の回折角
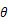 (ラジアン)には
(ラジアン)には
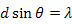 ・・・ ①
・・・ ①
の関係がある。ただし、
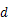 は回折格子の格子定数である。
は回折格子の格子定数である。
(1) 屈折率の計算A
図1のように、円形スクリーン上の0次の回折像と1次の回折像の弧の間隔を
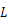 とし、円形スクリーンの半径を
とし、円形スクリーンの半径を
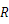 とする。
とする。
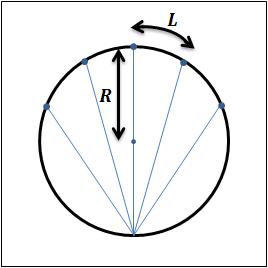
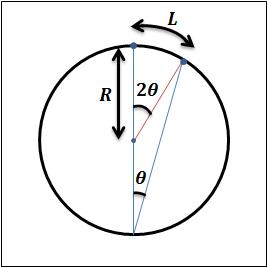
図1 回折像の模式図1 図2 回折像の模式図2
図2より回折角
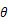 は
は
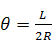 ・・・ ②
・・・ ②
①、②より、
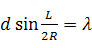 ・・・ ③
・・・ ③
が成り立つ。
同様の実験を屈折率
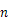 の液体中で行った場合、液体中の波長は
の液体中で行った場合、液体中の波長は
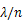 となるので、0次と1次の回折像の間隔は狭くなる。弧の間隔を
となるので、0次と1次の回折像の間隔は狭くなる。弧の間隔を
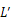 とすると、
とすると、
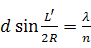 ・・・ ④
・・・ ④
が成り立つ。
③、④より屈折率
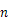 は
は
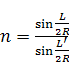 ・・・ (A)式
・・・ (A)式
と表すことができる。
(2) 屈折率の計算B(近似)
回折角
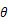 が小さい時、図3に示す0次の回折像と1次の回折像の直線距離
が小さい時、図3に示す0次の回折像と1次の回折像の直線距離
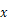 と、その弧の長さ
と、その弧の長さ
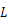 とがほぼ等しいものとみなすことができる。
とがほぼ等しいものとみなすことができる。
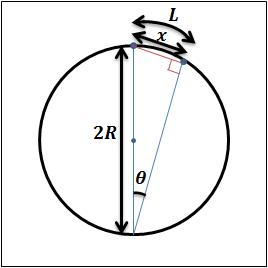
図3 回折像の模式図3
したがって、
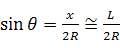
これを①に代入すると、
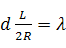 ・・・ ⑤
・・・ ⑤
同様の実験を屈折率
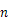 の液体中で行った場合、0次と1次の回折像の弧の長さ
の液体中で行った場合、0次と1次の回折像の弧の長さ
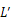 は、
は、
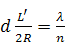 ・・・ ⑥
・・・ ⑥
⑤、⑥より屈折率
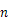 は、
は、
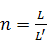 ・・・ (B)式
・・・ (B)式
と表せる。