ものさしによる回折を利用した光の波長の測定
1 はじめに
ものさしの目盛りに斜めからレーザー光線を当てると、反射した先に明るい点の列が観察できる。これは、ものさしには等間隔にすじ(目盛り)がつけられており、それを斜めから見た場合その間隔が非常に小さくなる。これが回折格子の働きをし、反射光が回折をおこし一定方向に明点を生じる。このことを利用して、レーザー光線の波長を測定することができる。
2 目的
ものさしの反射光による回折を利用してレーザー光線の波長を測定する。
3 原理
図1のようにレーザー光線をほぼ水平方向に出し、鉛直におかれたスクリーンに当てる。その照射点の位置をOとする。次に金属製のものさしをその目盛りのある面を水平の状態からスクリーン側の端を少し持ち上げ光線に当てる。このとき光線と目盛りの直線は垂直の状態になっている。するとスクリーン上には一番明るい点(P。とする)を中心として、上下方向に明点が並ぶ。この明点をP。に近いものからP1,P2 ・・・とする。
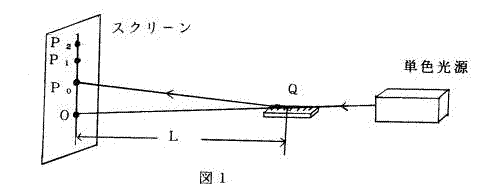
光線に沿って斜め方向からものさしの目盛りの線を見ると、これらの線は非常に狭い間隔で等間隔に並んでいる。光はきわめて短い波長を持つため、幅が1mm程度(ものさしの目盛り幅)のスリットでは回折現象のあらわれ方は小さい。しかし、光を斜めから当てることにより目盛りの間隔が見かけ上小さくなり、目盛りの線と線の間の部分が幅の狭いスリットの役目をし、このスリットでは回折現象のあらわれ方は大きくなる。
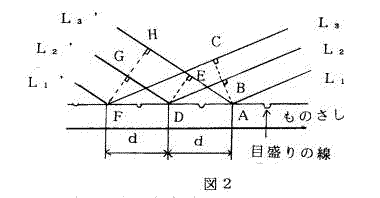
図2のように波長λのレーザー光線がものさしの面に対して角αで入射し、各スリットの対応点A,D,Fから回折して、ものさしの面と角βをなす方向へ進む平行な光を考える。図より光線LlL1'とL2L2'の光路差は
|BD−AE|=|d cosα−d cosβ|= d|cosα−cosβ|・・・ 1
である。他の隣り合った光の光路差も同じである。
したがって光が干渉して強めあう条件は
d|cosα−cosβ|= nλ( n=0,1,2,・・・)
となり、この条件以外のときは、各スリットの対応点からの光は少しずつ位相差を生じ、全体として打ち消される。
ところで、α,βが小さいときは、近似式
tanα≒sinα≒α (1−α)n≒1−nα
が成立するから
cosα=(1−sin2α)1/2≒1−sin2α/2
同様に
cosβ≒1−sin2β/2
したがって光路差 1 式は
d|cosβ−cosα|=d|sin2β−sin2α|/2
≒d|β2−α2|/2
=d|(β+α)(β−α)|/2
≒d|tan(β+α)・tan(β−α)|/2
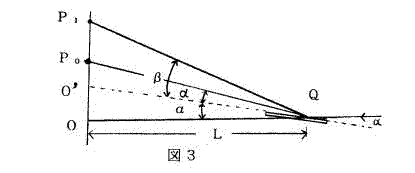
図3のように明点P。は目盛りに光を当てて得られたが、目盛りのない部分に光を当てても、反射によって同じ場所に明点が得られるので、P。はα=βとなる場合であり、このとき∠OQP0=2αとなっている。これは明点P。の条件式のnの値が0であることを意味している。
今、図3のように1次の明点(n=1)をP1とおくと、上で示した光路差の式において
tan(β+α)=OP1/L tan(β−α)=P0P1/L
が成り立つから、強め合う条件式はn=1のとき
λ=(d/2)・(OP1/L)・(P0P1/L)・・・ 2
と表される。ここで、OP1,P0P1,Lを測定すれば、光の波長λがわかる。
4 実験結果
はじめにレーザー光線を当てて点Oの位置に印をつける。次にレーザー光線の通路上にものさしの目盛りを当て、スクリーン上に明点を写し出す。点P・及び点P1に印をつけたうえで長さL,OP1,P0P1を測定する。次に測定結果を示す。
L=756cm OP1=54.9cm
P0P1=26.3cm
ここで使用したものさしは0.5mm目盛りであるので
d=0.5×10-3m
である。したがってレーザー光線の波長は
λ=(0.5×10-3/2)・(0.549/7.56)・(0.263/7.56)
=6.3×10-7m
次に、ここで行った実験のレーザー光線の入射角度αを各測定値より求めてみる。
図3より
tanα=(OP0/2)/L
=(28.6/2)/756
=0.0189
∴α ≒ 1°
また、図2より
d・sinα ≒ d・tanα
=0.5×0.0189
=0.00945mm
つまり、格子間隔が約0.0945mm(1mmあたり約100本の格子)の回折格子に相当する。
5 おわりに
本実験は格子間隔がわかっていて、光の波長を測定した。逆にレーザー光線の波長はわかっているため同様の実験をして格子間隔を求めることができる。よく使われる例として、CDやレコード盤の溝の間隔の測定実験があげられる。
本実験を、数回データを変えて実験を行ったところ、レーザー光線の波長を6.2×10−7 〜6.5×10−7mの範囲で求めることができた。
6 参考文献
旺文社:全国大学入試問題正解物理91年(p156〜157)