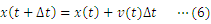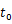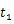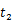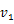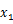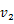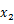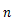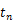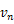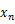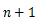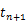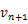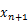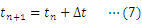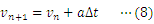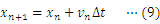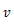重力を受けて落下する物体の運動方程式は次のように表せる。
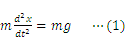
ただし,
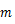 は物体の質量,
は物体の質量,
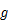 は重力加速度とし,空気抵抗は無視している。
は重力加速度とし,空気抵抗は無視している。
| この微分方程式を解くと,速度 |
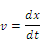
|
や変位 |
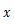
|
を時間 |
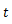
|
の関数として表すことができる。 |
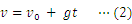
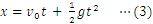
| ただし, |
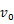
|
は初速度, |
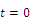
|
のときの変位 |
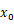
|
は0であるとする。 |
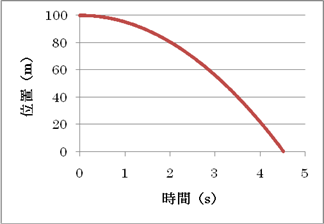
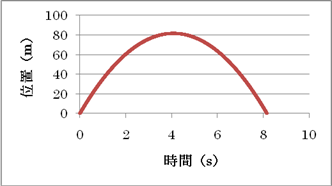
本研究では,(1)式をもとにしたシミュレーションを行うことで,微分方程式を解かずに,(2)式のような速度と時間の関係,(3)式のような変位と時間の関係が得られることを示したい。
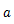
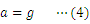
.png)
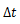
.png)
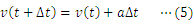
.png)
.png)