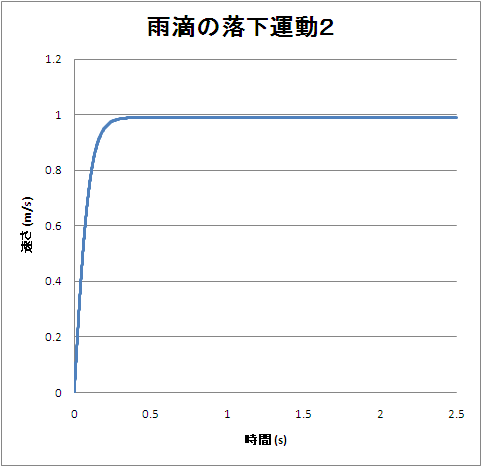
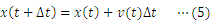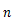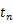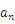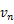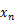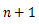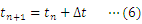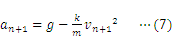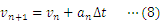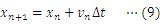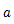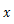空気抵抗がある場合の落体運動の代表例として,雨滴の落下運動が挙げられる。速度の2乗に比例する空気抵抗が雨滴にはたらく場合の運動方程式は次のように表せる。
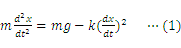
ただし,
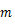 は物体の質量,
は物体の質量,
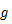 は重力加速度,
は重力加速度,
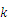 は比例係数とする。
は比例係数とする。
この微分方程式を解くと,速度
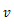 を時間
を時間
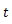 の関数として表すことができる。ただし,初速度を 0 とする。
の関数として表すことができる。ただし,初速度を 0 とする。
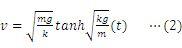
本研究では,(1)式をもとにしたシミュレーションを行うことで,微分方程式を解かずに,(2)式のような速度と時間の関係が得られることを示したい。ただし,本内容は「表計算ソフトを利用したシミュレーション2〜雨滴の落下運動1〜」を学習していることを前提とする。
.png)
.png)
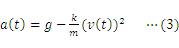
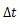
.png)
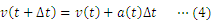
.png)
.png)