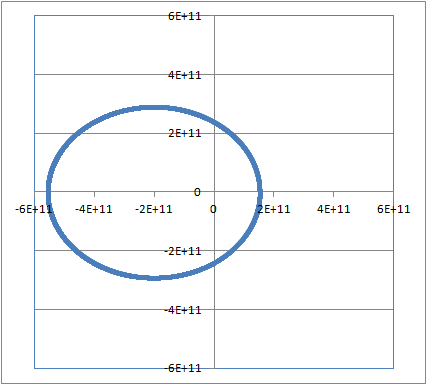
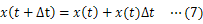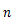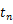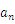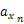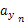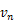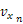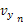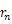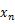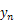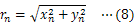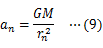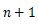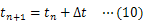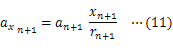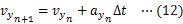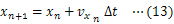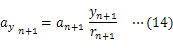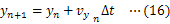物体に万有引力がはたらくときの運動方程式は次のように表せる。
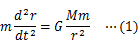
ただし,
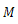 は原点とする物体の質量,
は原点とする物体の質量,
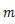 は原点まわりで運動する物体の質量,
は原点まわりで運動する物体の質量,
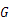 は万有引力定数とする。
は万有引力定数とする。
この微分方程式を極座標系で解くと,次のように
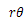 平面で運動する物体の軌道を求めることができる。
平面で運動する物体の軌道を求めることができる。
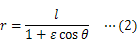
ただし,
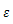 は離心率で,長軸半径
は離心率で,長軸半径
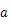 ,短軸半径
,短軸半径
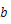 を用いて
を用いて
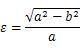
と表される。(2)式は
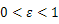 のとき楕円軌道を描く。
のとき楕円軌道を描く。
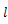 は,
は,
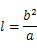
と表される。
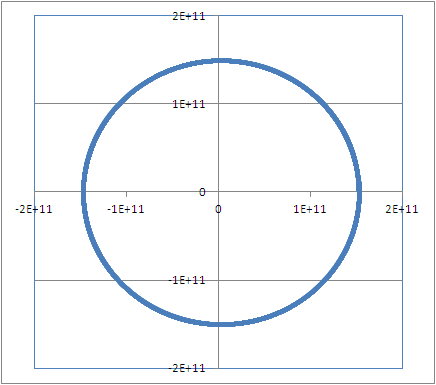
本研究では,(1)式をもとにしたシミュレーションを行うことで,万有引力を受けた物体の軌道を直交座標系で求め,それにより,ケプラーの法則を示したい。ただし,本内容は「表計算ソフトを利用したシミュレーション1〜モンキーハンティング〜」を学習していることを前提とする。
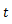
.png)
.png)
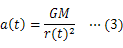
.png)
.png)
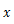
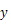
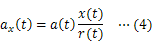
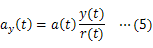
.png)
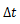
.png)
.png)
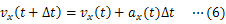
.png)
.png)