高等学校数学における観点別評価を取り入れた単元テストの作成
はじめに
観点別評価の考え方は浸透しつつあるが,学校での実践が順調に進んでいるとは言えない状況にある。それは,観点別評価の理念が,評価の在り方の見直しを求めるにとどまらず,結果的に授業方法の改善を迫るものだからである。その意味で,急速な改善は容易ではないが,高等学校における評価で大きな位置を占めている定期考査が,観点別評価の趣旨を踏まえて問題作成されることは,授業改善に向けた重要な一歩になると考えられる。
国立教育政策研究所「評価規準の作成,評価方法の工夫改善のための参考資料(高等学校)」(平成16年)には,数学基礎「(2)社会生活における数理的な考察」と数学Ⅰ「(2)二次関数」について,評価の具体的な進め方の例示があるが,考査問題や単元テストの例示は含まれていない。そこで,当センターの研究会では,考査問題の作成に当たって参考となるように,四観点の趣旨が生かされた評価問題について協議し,6種類の単元テストとしてまとめた。
1 観点別評価の在り方
(1) 観点別評価のよさ
四観点「関心・意欲・態度」「数学的な見方や考え方」「表現・処理」「知識・理解」は,数学の学習指導を明確に4分割するものではない。むしろ,教員が四観点を意識することにより,教材の取り上げ方や発問,生徒の取組に対する見方を豊かにする点によさがあると考えられる。
(2) 観点別評価の方法
国立教育政策研究所「評価規準の作成,評価方法の工夫改善のための参考資料(高等学校)」によれば,評価は授業と単元テストを通じて,「十分満足できると判断される状況」(a),「おおむね満足できると判断される状況」(b),「努力を要すると判断される状況」(c)の3段階で行われる。また,授業と単元テストとによる評価の総括においては,授業時の評価が単元テストと同等程度のウェイトをもつものとして扱われている。
一般に,評価規準は抽象的に表現されるが,この抽象性こそが生徒全員に対する評価を可能にすると考えられる。すなわち,一授業内の評価場面では,評価規準を具体化した「本時の基準」が必要であるが,評価規準そのものを具体的すぎる特定の活動結果として記述してしまうと,観察によって全員を評価することは物理的に不可能になる。数時間にわたる形成的な評価を行う前提として,評価規準は他の場面での評価が可能な程度に普遍的な表現であることが必要と言える。ただ,複数の教員が共通の評価規準に基づいて評価を行うに当たっては,運用に関する共通理解を図ることが重要な課題になる。
(3) 観点別評価における単元テスト
単元テストを観点別評価に位置付けるには,問題が観点別に構成されている必要がある。また,作業が繁雑にならないように,大問ごとに一つの観点が定められている必要がある。
従来は,むしろ様々な要素が融合的であることを良問の基準とする考え方もあったが,観点を意識することで,計算技能にこだわらない設問やより深く本質に迫る設問の工夫が必要になり,教員としての力量向上につながると考えられる。
2 観点別評価を取り入れた単元テストの作成について
(1) 単元テスト作成上の前提
国立教育政策研究所「評価規準の作成,評価方法の工夫改善のための参考資料(高等学校)」によれば,単元テストの評価規準は,授業におけるものをそのまま用いてもよいが,新たに作成してもよいとされる。ここでは,授業時の評価規準を用いるものとして作成する。
単元テストの各問題には,「評価規準」とともに「aの基準」(b又はcの評価だけを与える問題については「評価規準」のみ)を示しているが,数量化できるもの以外は抽象的で普遍性を保持した形で表現している。したがって,添付した評価規準と実際の採点基準とは一致する場合もあれば,一致しない場合もある。それは,各教員が生徒の実態に応じて1点刻みで与えた部分点を,「評価規準」と「aの基準」とによって3段階評価に解釈し直すには,この程度の表現に基づけば可能であると考えるからである。
一つの大問を,二つ以上の観点で評価する問題として出題することは,観点別評価の趣旨から慎重でなければならないが,関心・意欲・態度については,教育課程実施状況調査においても他の観点と重複する形で設定されており,観点の趣旨に沿った取扱いである限りは許容されると考えている。
単元テストは,指導と評価の全体計画の仕上げとして位置付けられるため,ここでは,数学Ⅱの単元「微分」における「指導と評価の計画」「授業の展開」「単元テスト」の一連の流れを例示する。
(2) 指導と評価の計画(例:「微分」(数学Ⅱ)全13時間)
|
|
| |
授業内容 |
学習活動における具体の評価規準 |
評価方法 |
第1時
|
平均変化率と微分係数の意味
・具体的な課題を提示する。
|
・平均変化率と微分係数の意味に関心をもち,接線の傾きの考察に,極限値を活用しようとする。(関心・意欲・態度) |
観察
(ノート提出)
|
第2時
|
導関数
・導関数の計算をする。
|
・関数の和,差及び定数倍の導関数について求めることができる。(表現・処理) |
観察
(ノート提出) |
第3時
~
第4時
|
接線の方程式
・接線や法線の方程式を求める。
・曲線外の点から引いた接線の方程式を求める。 |
・接線の方程式の求め方について理解し,接することの定義を正確に身に付けている。
(知識・理解)
|
小テスト
|
第5時
|
関数の値の増加・減少
・f´(x)の符号と関数の値の増減及び極大・極小との関係を理解する。 |
・3次関数の値の増減について,接線の傾きなどと関連付けて考察することができる。
(数学的な見方や考え方) |
観察
|
第6時
|
・3次関数のグラフをかく。 |
・f´(x)を利用して,f(x)の増減を調べ,グラフをかくことができる。(表現・処理) |
観察
(ノート提出) |
第7時
|
・3次関数を決定する。
|
・極値に関する条件から,3次関数を決定することができる。(表現・処理) |
観察
(ノート提出) |
第8時
~
第9時
|
・3次関数の最大値と最小値を求める。
・具体的な課題を提示する。
|
・3次関数の増減表を用いて,3次関数の最大値・最小値を求めることができる。
(表現・処理)
・日常の事象との関連を踏まえ,具体的な事象の考察に3次関数の最大・最小を活用しようとする。(関心・意欲・態度) |
観察
(ノート提出)
観察
|
第10時
~
第13時
|
方程式・不等式への応用
・3次方程式と3次関数の関連を考える。
・3次方程式の実数解の個数を調べる。
・3次不等式への応用を考える。 |
・3次方程式の解を3次関数のグラフを用いて考察することができる。
(数学的な見方や考え方)
・3次関数のグラフを活用して,3次方程式の実数解の個数を調べることができる。
(表現・処理)
・3次関数のグラフを活用して,3次不等式の問題を考察することができる。
(数学的な見方や考え方) |
観察
観察
(ノート提出)
観察
(ノート提出)
|
|
※ノートには,ワークシートも含む
(3) 単元テストを作成する前提となる授業の展開と評価(例:「微分」(数学Ⅱ))
単元テストを作成する際には,授業内容や平素の評価がどのように行われているかと切り離して考えることはできない。単元テスト作成の前提となる授業展開と評価を以下に整理した。
ア 微分係数と導関数
①微分係数 ・・・ 微分係数の概念を導入するための極限計算については,数学Ⅱにおいては深入りしない。
②導関数 ・・・ 具体的な関数の微分演算については,授業時の観察やノート提出によって評価を行うため,単元テストで問うことはしない。
イ 導関数の応用
①接線 ・・・ 接することの定義が正確に理解されているかを問うために,y=x3 の原点における接線について確認する。
また,曲線外の点から接線を引く場合については,理解が不十分な生徒がいるため,再度確認する。
②関数の増減と極大・極小
・・・ 具体的な3次関数の増減を調べてグラフをかくことは,授業時の観察やノート提出(観察)によって評価するため,単元テストで問うことはしない。
単元テストにおいては,関数f(x)の増減(極値の存在)を調べるために,導関数f´(x) をいかに利用するかという,数学的な見方や考え方に注目して問う。
また,「f´(a)=0 ⇒ x=aでy=f(x)は極値をもつ」が常に成り立つわけではないことを強調する。
③関数の最大・最小
・・・ 区間で定義された,具体的な3次関数の最大・最小は,授業時の観察やノート提出によって評価するため,単元テストで問うことはしない。
単元テストでは,関心・意欲・態度の観点も含めて,最大・最小問題の読解・考察に3次関数を活用しようとするかどうかを問う。
④方程式・不等式への応用
・・・ 実数解の個数に関する分類については,授業時の観察やノート提出によって評価するため,単元テストで問うことはしない。
単元テストでは,実数解の符号まで調べさせることにより,グラフの共有点のx座標と方程式の実数解とを対応させることができるか確認する。
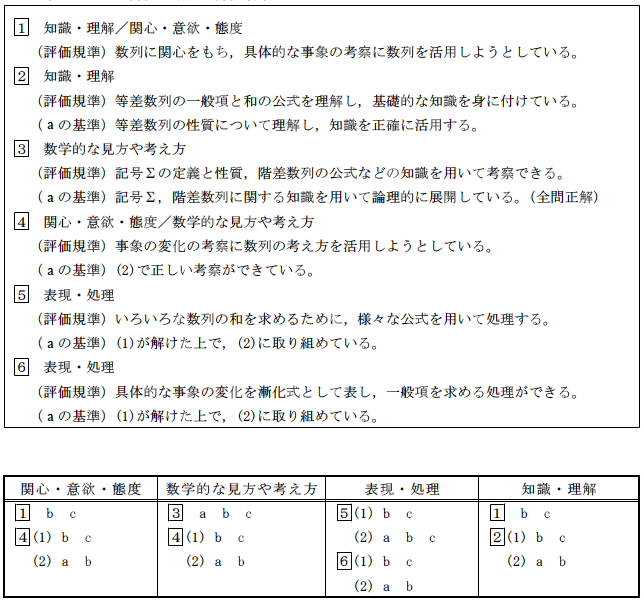
(4) 単元テスト(例:「微分」(数学Ⅱ))

(5) 単元テストの評価の観点と評価規準(例:「微分」(数学Ⅱ))
単元テストの評価規準は,授業時と同じものを用いる方法と別に作成する方法とが考えられるが,ここでは,単元テストの評価規準を作成する方法で考えている。

ここで,図の a b c は,一つの問題でabc の判断をする問題であることを意味し,b c はbc の判断をする問題であることを意味している。
3 「三角比」(数学Ⅰ)の単元テスト
(1) 単元テスト
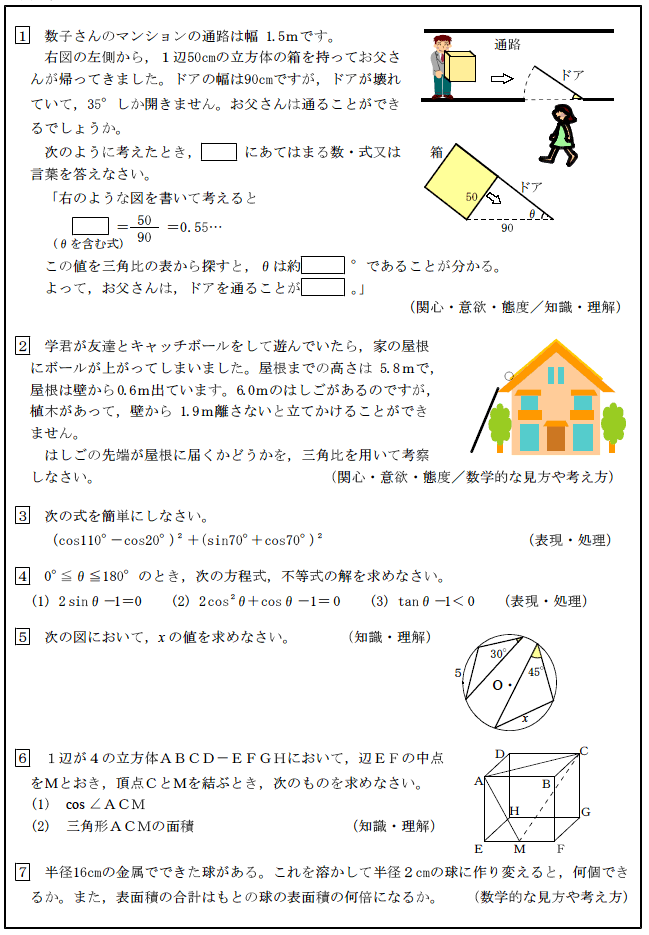
(2) 単元テストの評価の観点と評価規準

4 「確率」(数学A)の単元テスト
(1) 単元テスト

(2) 単元テストの評価の観点と評価規準

5 「方程式・式と証明」(数学Ⅱ)の単元テスト
(1) 単元テスト

(2) 単元テストの評価の観点と評価規準

6 「図形と方程式」(数学Ⅱ)の単元テスト
(1) 単元テスト
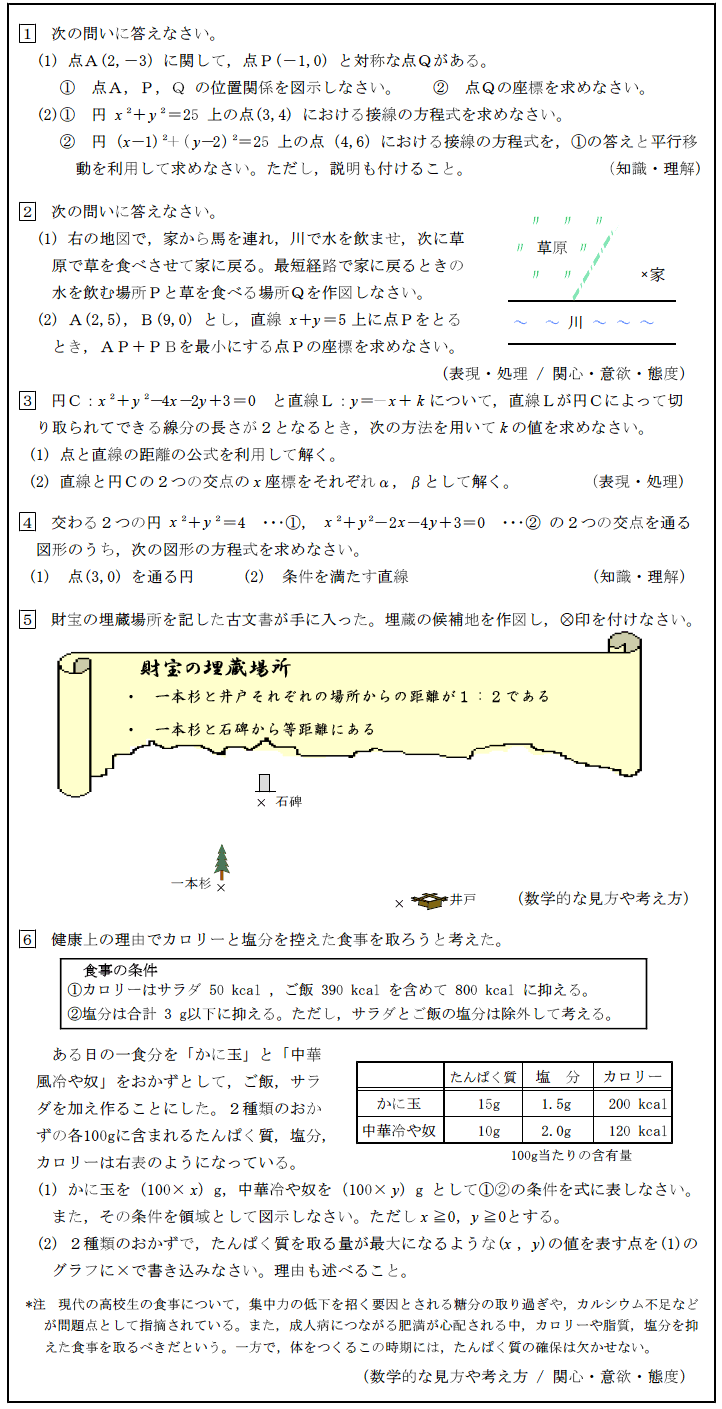
(2) 単元テストの評価の観点と評価規準

7 「数列」(数学B)の単元テスト
(1) 単元テスト

(2) 単元テストの評価の観点と評価規準