|
4 分析結果の概要 |
|
| (1) 図形に関する問題に課題 | |
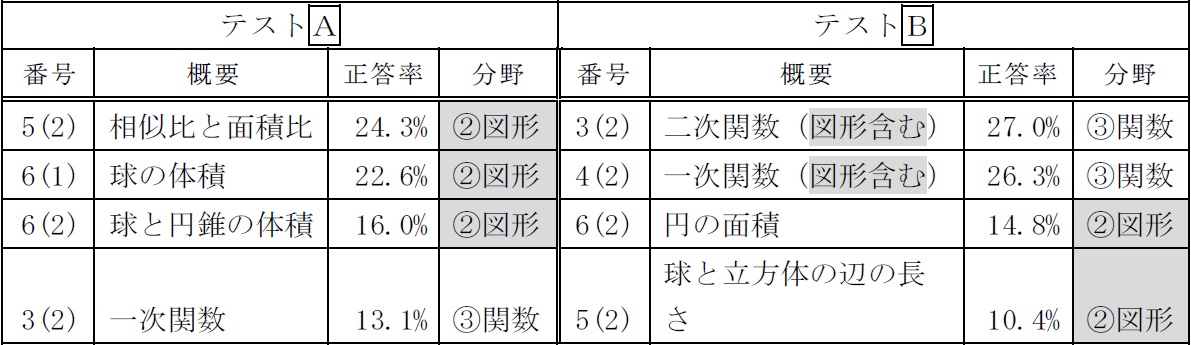
| 毎年,図形に関する問題を出題しているが,その正答率は,昨年度に引き続き低く,30%を下回っている。表4は,テストA,テストBの正答率が30%を下回った問題である。テストA,テストBともに,図形に関する問題の正答率が低いことが分かる。特に,円の面積や球の体積に関する問題と図形の相似比と面積比に関する問題の正答率が低い。他の図形の問題については,三角形の内角と平行線の同位角に関する問題(テストA1(13))や,円周角と中心角に関する問題(テストB1(11))は,高い正答率であった。 正答率の低かった問題の共通点は,今回の学習指導要領の改訂により,高等学校から中学校に移行した学習内容であるということである。球の表面積と体積については,中学1年で,相似な図形の面積比と体積比については,中学3年でそれぞれ学習することになっている。図形の問題は,特に立体図形など,イメージすることが難しいという特徴がある。具体的にイメージできるように教材や教具を工夫する。例えば,模型を示す,ICTを活用するなどの方策が挙げられる。 中学校の先生方と情報交換をしながら対策を検討する必要がある。 |
|
表4 |
|
 |
|
(2) 二次方程式の解を求める問題に課題 |
|
| 二次方程式の解を求める問題は,テストA,テストBともに出題した。正答率は,テストA1(8)で32.6%,テストB1(6)で69.3%であった。 二次方程式の解の公式は,今回の学習指導要領の改訂により,高等学校から中学校に移行した学習内容である。テストA1(8)は,因数分解,解の公式をすぐに使うことができない式であったこと,テストB1(6)は,解の公式は利用したが,分数式の約分でミスをしてしまったことで上記のような正答率になったと考えられる。 二次方程式の解法の手順の定着については,フローチャートを用いるなど,きちんと整理して指導する必要がある。また,分数式の約分のミスについては,計算過程を丁寧に書かせる指導を徹底して行うことが大切である。 |
|