Ｈ19～21の２次方程式に関する問題・正答率を表13にまとめた。上位群は例年正答率が高いが，下位群の正答率は，Ｈ19の90％に対して，Ｈ20，21はそれぞれ66％，59％と大きく下回っている。その原因は展開・整理後の２次方程式の形にあると考えられる。
　Ｈ21についてはx＝2 という誤答が12.7％あり，その誤答の原因としては，式変形をしてx^２＝4 となったときに，「x は2乗したら4だから･･･ 2だ」と簡単に考えてしまったことだと思われる。これは，x^２＝k (k ＞0) 型の方程式の解が√kと－√kの２つがあるという基本が十分定着していないことに起因しているといえる。この誤りは，例年Ａ問題やＴ問題でも多くみられるものである。
　Ｈ20についてはx＝12という誤答が5.6％あり，その原因として次の①～③の場合が考えられる。

　２次方程式の指導の大きな流れとしては，与式をax^２＋bx＋c＝0の形にした後，因数分解するか，それが不可能ならば解の公式を利用して解くというものである。Ｈ21のx^２＝4についても因数分解に習熟していればx^２－4＝0として(x＋2)(x－2)＝0と解くこともできるが，x^２＝4は「２乗したら４になるようなxを求めよ」と式を言葉に翻訳させ，それはすなわち「４の平方根」を求めることだと意識させたい。そして，そのときに平方根は正と負の２つあるという基本をここで再確認させたい。
　因数分解できる方程式についても，機械的に解を求めさせるのではなく，「ＡＢ＝0ならばＡ＝0またはＢ＝0」という根底に流れる内容をつかませた上で解かせたい。

 [１]（6）はさいころに関する確率の問題である。さいころの問題については，中学において必ず取り上げられる内容であり，無答率は低いが正答率は59.3％と決して高いとはいえない。誤答としては，2／9が11.3％であった。２つのさいころについての問題なので，すべての場合の数は36通りで，b／aが奇数になるのは９通りであるが，先に挙げた誤答は数え漏れがあり，b／aが奇数になる場合を８通りとしたものと考えられる。

　ある事柄の起こる確率は，対象の事象をいかに「漏れなく・重複せず」数え上げるかが肝要である。方針を立てず思いついた順に数えるのではなく工夫が必要である。基本的なものとしては樹形図や表であり，本問については右のような表を作ることで漏れなく数えられる。
　高校においての場合の数・確率というと，公式_nP_r，_nC_rを使って解く問題が多くあるが，数え上げは場合の数・確率の基本となるので丁寧に指導していく必要がある。

ここ数年，変域に関する問題は２次関数を題材として出題し，60％の正解率であった。今回は，反比例のグラフを出題したところ，同じ傾向の問題であるにもかかわらず，正答率は48%であった。
　誤答について見てみると，グラフをイメージせずに，「xが最小値のとき，yも最小値をとる」と考え，x＝3のとき，y＝2であるとして解いたa＝6という誤答が全体の28％もあった。

昨年の分析にも「関数f(x)が単調増加ではない場合に，グラフを利用することが有効」と述べたが，グラフのイメージができない生徒は，今回のような定義域・値域の問題を間違えやすい。このような生徒に対する指導が今後の課題である。
　今回その一つの方法として提案するのが，プロジェクターや電子黒板などに代表されるＩＣＴ機器と，過去にも紹介したGrapesなどに代表されるグラフツールの活用である。その利点としては，①変化の様子を動的に表す事が出来る，②正確なグラフが瞬時に示せる，などが挙げられる。
　活用例としては，Grapesがサンプルとして最初から持っている２次関数の最小値を表示する機能の利用などが挙げられる。変化の様子を動画などで見せて説明すれば，理解が進む場合もあるだろう。また生徒自身が操作して，最大値や，最小値の変化の様子を調べる等，工夫次第ではいろいろな授業展開が可能である。

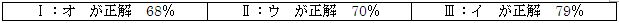　Ⅰ，Ⅱ，Ⅲの中ではⅢが最も正答率が高かった。また，ⅠまたはⅡが不正解でⅢが正解だった割合は全体の22％にのぼり，この中の多くは証明の結論「△ＤＰＣ＝1/2△ＡＢＣ」と直前の「（Ⅲ）＝△ＤＰＣ」を見比べてⅢの面積が△ＡＢＣの半分であることに気づき，イを選択したものと考えられる。すなわち結論から逆にたどって導いたと考えられる。
　［４］(2)の正答率は(1)に比べ低かった。三角形の相似の関係からＰＭを求め，ＢＭから引けばよいのだが，気づかなかった者が多かったようである。1.5及び2という誤答は台形ＡＰＭＤをＡＤ＝ＰＭの等脚台形だと見た目で判断したことが原因と考えられる。また，見た目から1と答えた者も多かった。

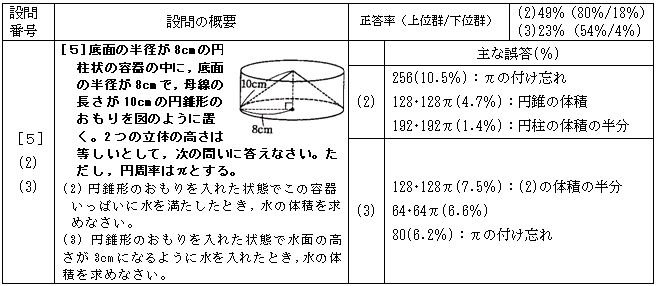
［５］(2)(3)は立体の体積を求める問題である。いずれもπをつけ忘れた誤答が多かった。(3)の64πは(1)の答から円柱の体積の半分を除いた後に，円錐の上部の体積を加え忘れたものであった。
　上位群と下位群で正答率の差が大きいことと，テストＡ［５］(2)の正答率が低いことから，下位群の中には円錐の体積を求める段階からつまずいている者も多いと考えられる。