５　調査問題の妥当性と信頼性(Ｓ−Ｐ表等による分析)
　平成25年度高等学校入学者数学学力調査Ａ，Ｂについて，Ｓ−Ｐ表処理等を基にして差異係数，信頼性係数，内容別平均正答率，正答率帯別問題数，注意係数，ＵＬ指数，問題間の相関等を考察したところ，次のような結果を得た。なお，データは，テストＡについては参加31校から244名，テストＢについては116校から1,472名を抽出して作成した。

[１]　問題全体について

(1) 差異係数	表５
差異係数とは，Ｓ，Ｐ両曲線のずれの程度を数量化したもので，生徒理解と一連の学習内容がうまくかみ合っているかを見るものである。差異係数は０から１の値をとり，0.5より小さい値のとき生徒の理解と指導の密着性が高いとされている。
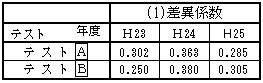簡単な確認テストのようなドリル演習型のテストではＳ曲線とＰ曲線の乖離は小さく，差異係数は小さくなる。実力テストのような多面にわたる総合的な問題ではＳ曲線とＰ曲線は大きく乖離して，差異係数は大きくなる。差異係数が0.5を超えたとき，指導内容に問題がなかったか，出題に問題がなかったか，学習者の理解やモチベーションはよかったかなどを検討する必要がある。今回のテストでは表５のように差異係数は小さいので，出題及び学習者の理解の間にとりわけ大きな問題はないと考えられる。

(2) 信頼性係数（クーダー・リチャードソンの公式20による）
信頼性係数とは，作成されたテスト問題が内容的に妥当で信頼できるものなのかを算出するものである。ここで言う信頼性とは，同一条件下で再度試験を実施しても同じ結果が出ると思われる安定性のことで，０から１の値をとり，１に近いほど信頼性が高いとされている。	表６
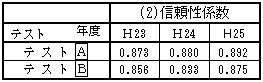今回のテストでは表６のように信頼性係数は高いので，信頼できる良好な問題であったことが分かる。

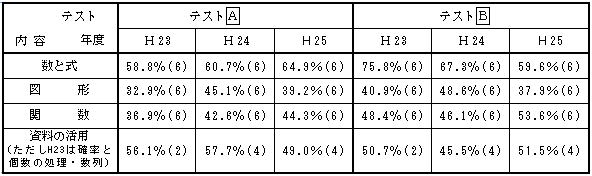
(3) 内容別平均正答率　( )内の数字は問題数 　Ａ，Ｂともに関数の分野において正答率が下がっている。詳細な分析については32ページ以降を参考にしていただきたい。

表７

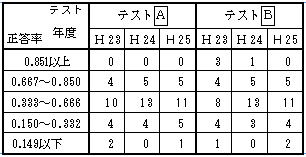
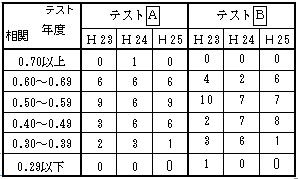
(4) 正答率帯別問題数　　　表８	(5) 全体の正答率との相関　　表９

[２]　検討を要する問題群

　　×印は該当項目について検討を要する数値であることを示す。　　　　表10
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

(各項目の説明)		表11
�@正答率	各問題の正答率を示す。
�A注意係数	ＳＰ表において，ある問題の正誤の状況と他の問題の正誤の状況を比較し，異質の程度を数値化したものである。0.5より小さい方が適切な問題であるとされている。表11に示すように平均正答率と併せて検討するとよい。
�BＵＬ指数	（上位27％の正答者数）−（下位27％の正答者数） 　　　　　　　　　（生徒27％の人数） 　ＵＬ指数は上式で算出する。「上位群に正答者が多く，下位群に正答者が少ない」場合にＵＬ指数は高くなるが、上位群に正答者が少なく下位群に正答者が多いという逆転現象の場合，ＵＬ指数は低くなる。ＵＬ指数が0.4より大きい方が適切な問題であるとされている。
�C相　　関	生徒の得点合計とその問題の正解との相関を示す。基準値を0.4として大きい方が適切な問題であるとされている。