|
(3) 動点の位置によって求める関数が異なる問題について理解を深めさせたい
|
 |
|
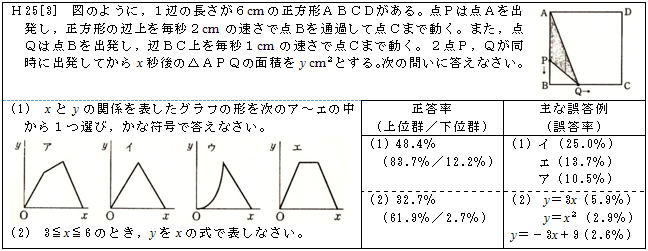
例年，動点や定点等を結んで図形をつくり，その面積を求める問題を出題している。Ｈ22，Ｈ23は(1)で具体的な場合の面積を求めさせ，(2)でそれを踏まえて，あるxの範囲でのxとyの関係式を求めさせた。しかし，Ｈ25では(1)で正確に立式をできなくても，xの範囲によってグラフが２次関数になるか１次関数になるかが分かれば，xとyの関係を表すグラフを選択できるという問題を出題した。上位群の正答率は80％を超えたが，全体として50％弱に留まった。
|
|
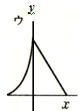
(2)は例年と同じ出題形式であるが，上位群の正答率も全体の正答率もあまり変化はみられなかった。主な誤答例の y＝－3x＋9と答えたのは，x＝3のとき面積９cm２，x＝6のとき三角形が存在しないので面積０cm２となるので傾きが－３，さらに右のグラフのように，x＝3の位置にy軸をもってきてy切片９として解いたと考察できる。
|
 |
 |
|
【今後の指導に向けて】
|
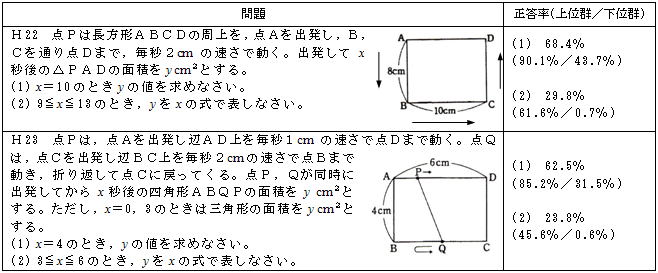
Ｈ22，Ｈ23において，具体的なxの値を与えたときyの値を求めることは60％以上できているので，動点が頂点を通過するとき，関数の式が変化する可能性があることに気付かせたい。また，場合分けするxの値の範囲が問題文の中に最初から指定されていない場合でも，動点が頂点を通過するときに注意すれば，自分で場合分けするヒントになる。この種の問題では，次の手順で考えると分かりやすい。
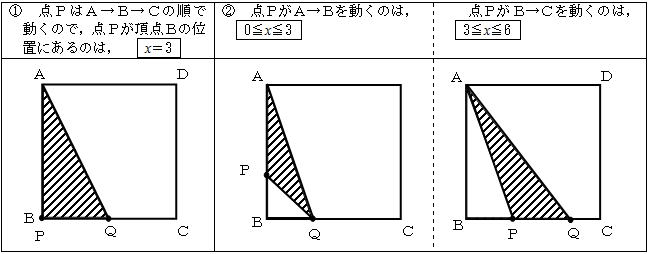
① 通過する頂点に動点があるときのxの値を求める。
② 求めたxの値の前と後の図形における面積を考える。
|
|
③ x秒後の辺の長さをそれぞれ求める。
0≦x≦3のとき ＡＰ＝2x ，ＢＱ＝x
よって求める面積は y＝x２
3≦x≦6のとき (Ａ-Ｂ-Ｐ)＝2x ，ＢＱ＝x
ＢＰ＝(Ａ-Ｂ-Ｐ)－ＡＢ，ＰＱ＝ＢＱ－ＢＰ
ＢＰ＝2x－6， ＰＱ＝x－(2x－6)＝－x＋6
よって求める面積は y＝－3x＋18
|
※ ＡからＢを通ってＰまでの距離ＡＢ＋ＢＰを以下のように表記した。
(Ａ-Ｂ-Ｐ)
|
|
(4) 空間図形をいろいろな見方ができるようにしたい
|
 |
|
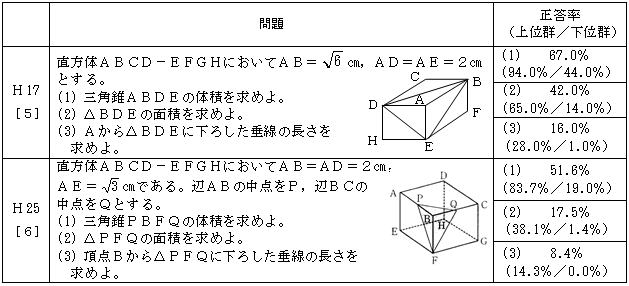
直方体から三角錐を切り取り，その高さを求める問題を８年ぶりに出題した。(1)の三角錐の体積は正答率が67.0％から51.6％に大きく下がった。(2),(3)は分数計算ということもあり正答率はさらに下がった。空間図形の問題を苦手とする生徒が増えているので今まで以上に丁寧な指導が必要である。
|
|
【今後の指導に向けて】
|
|
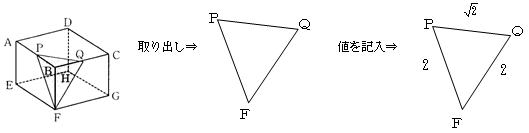
空間図形の問題を考える場合，必要な図を取り出して考えるのも良い方法である。今回の問題の(2)は，切り口の△ＰＱＦを描き，各辺の長さを求めると，二等辺三角形の面積を求めればよいことが分かる。
|
|
|
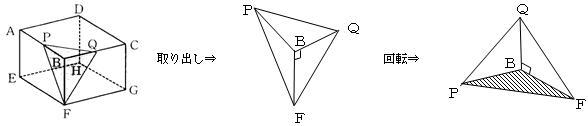
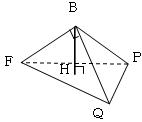
また，(1),(3)の四面体の問題でも同様に，四面体を取り出し，条件を書き込んで，状況を把握しやすくして問題に取り組むとよい。また，図形を回転させたり，底面に薄く色を付けたりして，状況を把握しやすくすると，解く方針が立てやすくなる。
|
|
|
また，１つの図形で別な見方をする習慣を身につけさせるために，いろいろな面を底面と考えて体積Ｖを計算する練習を取り入れるのも効果的である。具体的には，
|
|
|
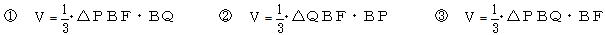
をそれぞれ計算させ，その後△ＰＦＱを底面として考えることで，高さＢＨを求める計算へと誘導したい。
|
|
と
等の違いを理解しているかを確認する問題で，Ｈ24は２乗される数を分数にし，Ｈ25は小数にして，その結果にどれだけ違いが出るか調査した。分数計算を含めたＨ24は，Ｈ20やＨ23と比較して，正答率は約７ポイント下がった。小数計算を含めたＨ25は，Ｈ20やＨ23と比較して，正答率は27ポイント下がり，下位群の正答率は50ポイント近く下がった。
は，
を1.6と計算したもの，誤答13は，