| (1)
グラフを活用する大切さを育てたい
|
 |
|
(1)は水の増加量を読み取り, x と y の関係を1次関数で表す問題で,(2)は(1)の結果を利用して x の値を求める問題である。しかし,正答率は(1)より(2)の方が高い結果になった。これは,25㎝から既に入っていた5㎝を引き,その結果を1分当たりの増加量である2で割れば答えが出せるためである。このことに気がついた生徒は,(1)の式ができていなくても(2)で正答を導くことができたようである。
|
| 【今後の指導に向けて】 |
(1)が解けなくても,あきらめず(2)に取り組んだ生徒がいたことは良かったといえる。しかし,今回のように,式を立てることが出来なくても値を出せるという方法は,常に通用するものではないので,条件から式を立てることができるように指導しておく必要がある。特に,高等学校の数学では文字を扱うことが多く,立式しないと解けない場合があるので,立式する方法を確実に身に付けさせたい。
問題文の「一定の割合」という言葉や誤答の結果から,答えが1次関数であるということは理解できているようである。よって,その1次関数を,y=ax+b
とおくことを習慣にさせたい。また,増加量が2であることから1次関数の傾きが2と分かったのだが,はじめに入っている5㎝の部分を切片として考えることができず,y=2x
としてしまった生徒が13.9%いた。これも最初に y=2x+b とおき,(0,5)を代入して b を求めるという手順で解けば,切片を忘れるという誤答も減らしていけると思われる。
また次のように,1分後,2分後・・・の結果から,関数を類推して求め,最後に立てた式が合っているか確認する方法も紹介すると,更に定着を図ることができる。
|
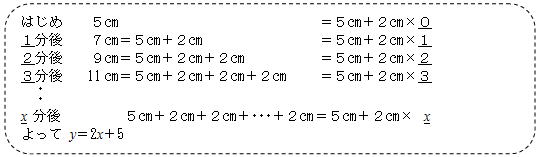
|
(類題)長さ10㎝のバネがあり,5gのおもりをつるすと25㎝になる。x g のおもりをつるしたときのばねの長さを y ㎝とする。次の問いに答えなさい。
(1) y を x の式で表しなさい。
(2) バネ全体の長さが40㎝ になるのは何gのおもりをつるしたときか求めなさい。
(解答)
(1) 5gで15㎝伸びるので1gで3㎝ の割合ということを読み取り,y=3x+b とおく。 (0,10)を代入すると 10=3×0+b よりb=10 したがって y=3x+10
(2) 40=3x+10より,x=10 したがって 10g
|